The impact of physics on designing autonomous systems

A personal journey towards designing autonomous buildings

Certainly, here is a possible introduction for your newsletter about buildings and AI¹. In the previous newsletter article, we discussed how data can be used to design autonomous systems. The conclusion was that data alone is hardly ever the answer for physical phenomena, governed by complex differential equations.

However, we can significantly reduce the necessity for vast amounts of real data in two ways:

1. Generated synthetic data

2. Integrating physics directly into the machine learning model

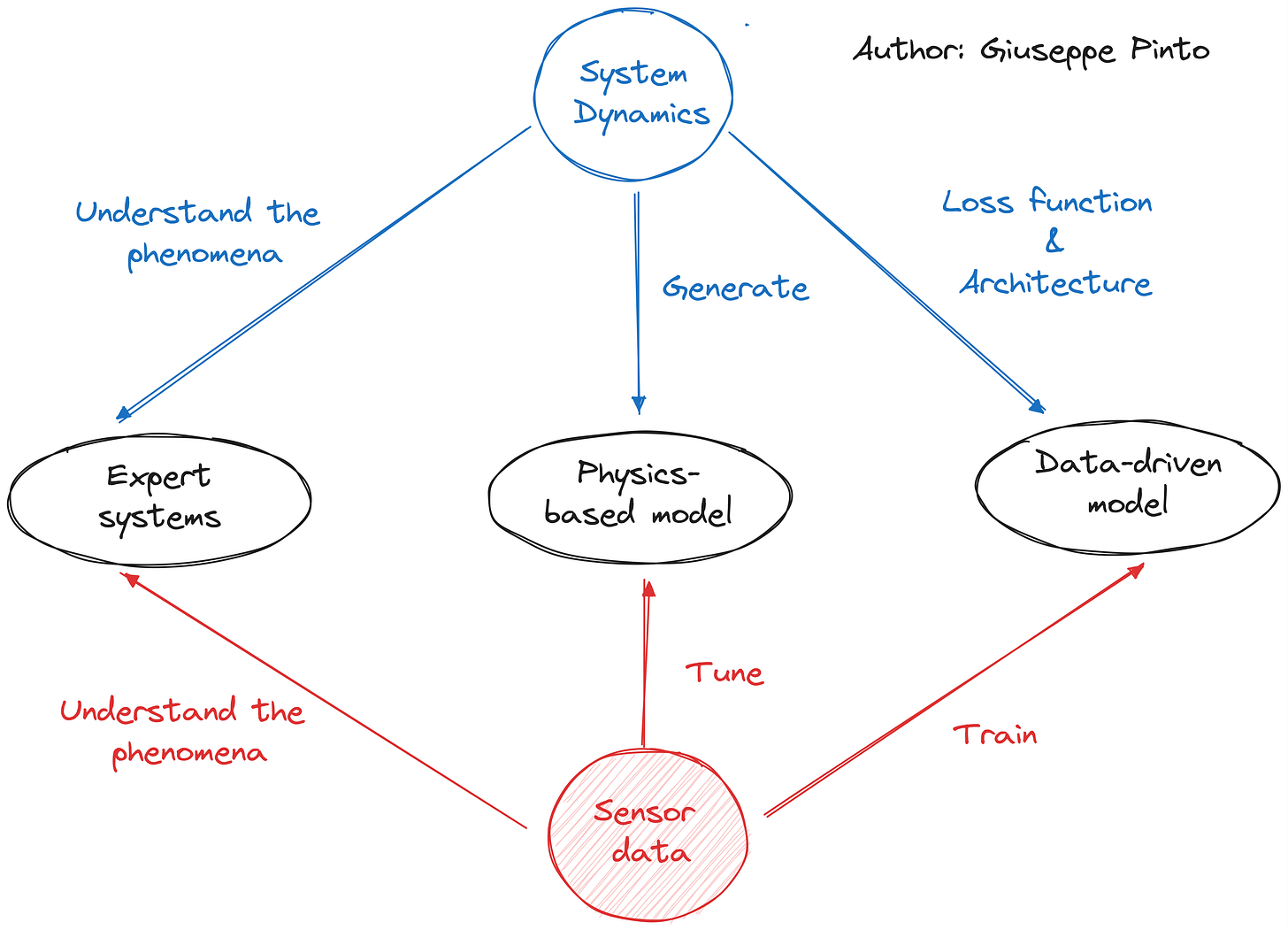
The caveat is that in order to generate synthetic data, or embed the physics into our machine learning model, we need to know the underlying rules of our phenomena. While these rules are generally well-established, their application demands considerable computational resources, time, and is typically tailored to a specific case study.

When managing projects worth hundreds of millions of dollars or overseeing mass production, these expenses are justifiable. However, for heterogeneous or small projects (like the vast majority of buildings) a detailed simulation can become prohibitive. It is crucial to remember that models should have a purpose (design, operation, or a mix of both) and represent realistic conditions. Here “realistic”does not necessarily imply events that will definitely occur, but rather, scenarios that adhere to physical laws.

Overcoming real data limitations with physics

If we want to get better results, we need to generalise beyond the training data we have, pushing new boundaries. This process inherently involves exploring uncharted paths (extrapolating), which can cause standard machine learning models to falter if not properly constrained or "guard-railed."

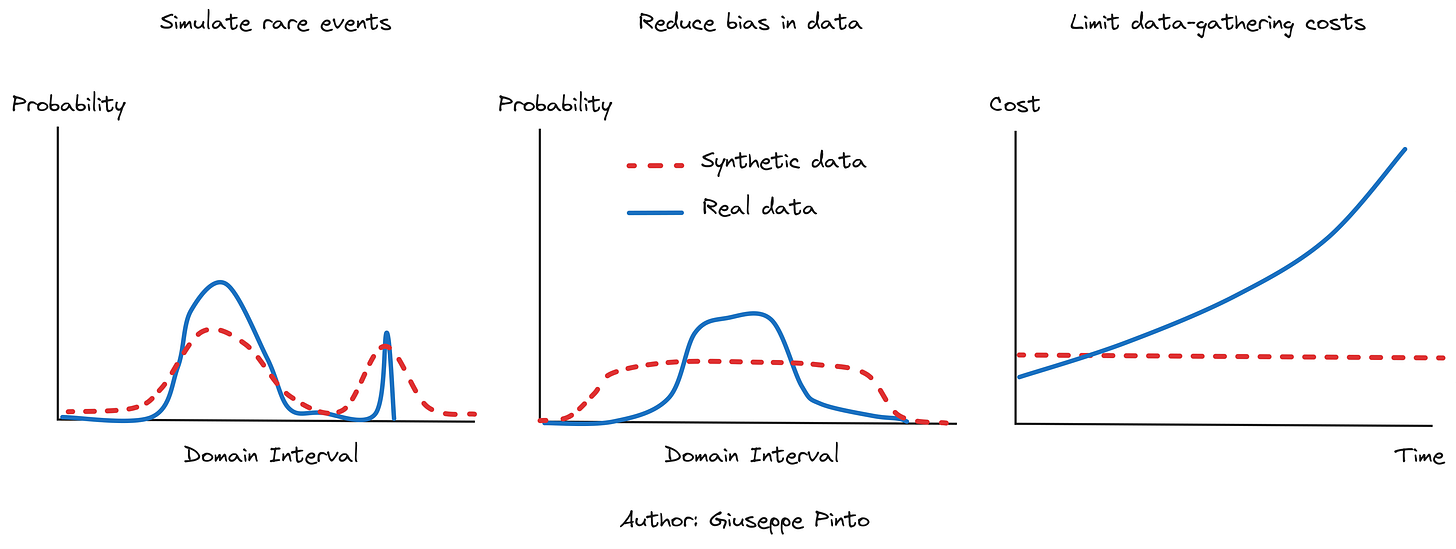
Consequently, the costs of generating synthetic data or incorporating physics into machine learning models are offset by the benefits of producing more reliable models. The key advantages of blending physics with data include mitigating issues related to data scarcity across specific domain intervals, addressing biased data, and reducing the expenses involved in data collection.

1. Rare events are… rare indeed, which means data is limited. However, by understanding the physics underlying this data, we can simulate rare events and identify the best responses to these situations. The caveat is that a lot of rare events have also unknown dynamics and this makes the problem harder to simulate.

2. Real data is usually biased to our preferred outcomes (comfort conditions in a building). However, it is crucial for a model to be able to represent a wide spectrum of conditions, representing the true “shape of the dataset”.² An internal temperature sensor will almost always work around the comfort band, while we might be interested in exploring other areas.

3. Data is expensive. In certain fields, collecting data may be impractical due to expenses or time constraints, making simulation a preferable alternative. In buildings, this phenomena is especially related to the seasonality of control. In order to gather 1 year of cooling data, we would probably need between 2 and 4 years of data.

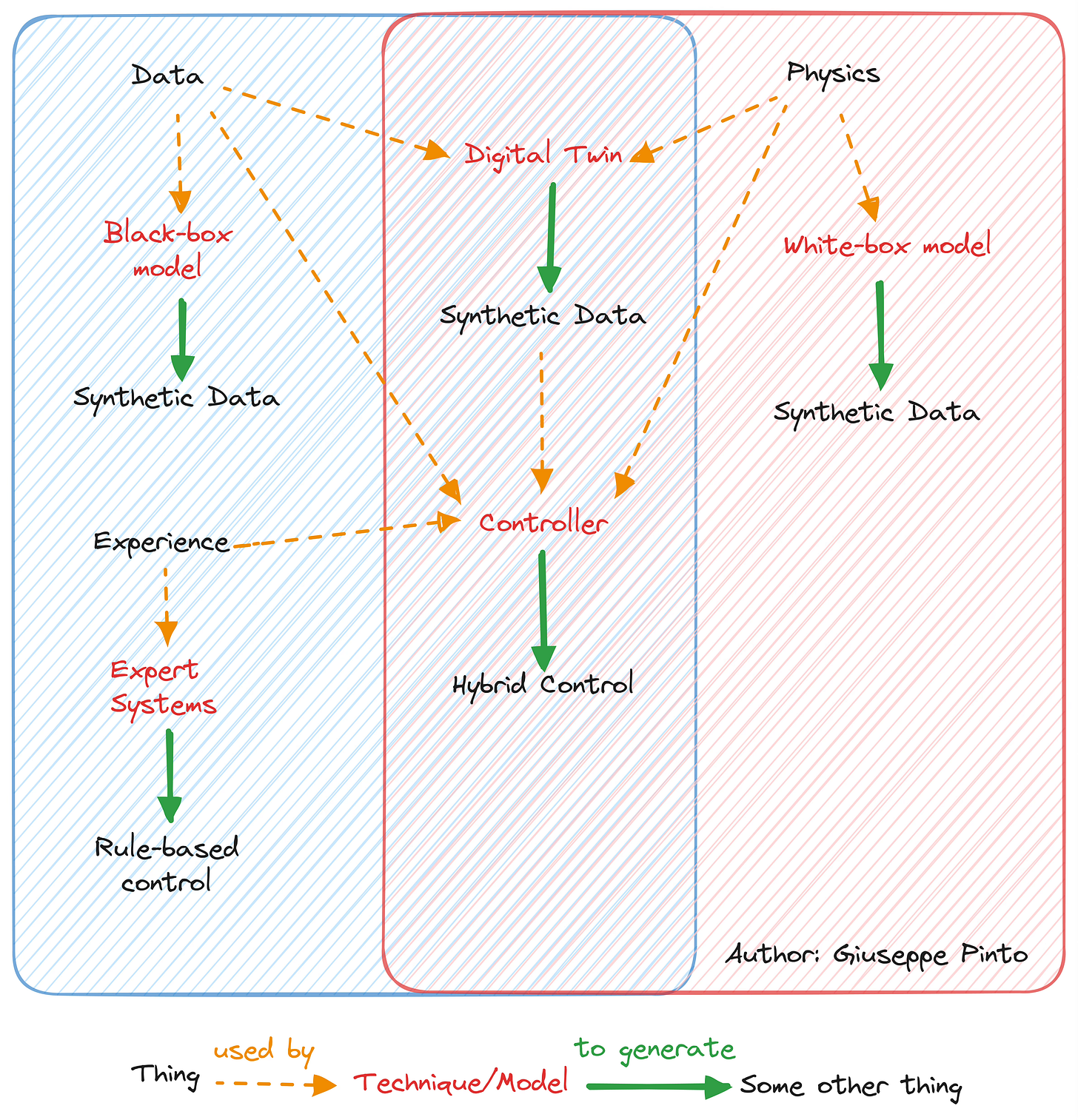
Generate synthetic data and embedding physics

There are substantial differences between the three way of generating data, mainly based on the goal we have and the problem at hand.

Generate synthetic data using a machine learning model

Broadly speaking, a machine learning model offers a fast inference and might be ideal to simulate complex interactions in real-time. This allows to generate synthetic data quickly.

However, no one said that we can only use sensor data to train a machine learning model. If detailed knowledge of the system is already available, a possible solution lies in generating a large amount of synthetic data using a physics-based model, and then training a machine learning model combining real and synthetic data, achieving fast inference while not being bottlenecked by the real-data acquisition process.

Generate synthetic data using a physics-based model

A physical representation of our system, especially if we are talking about an engineering system, should be the most accurate representation possible, putting black-box models out of jobs. However, the reality is that minor differences between components and their interactions can result in significant discrepancies between simulations and actual systems.

A viable solution involves calibrating our physical model using real data. To achieve a detailed and accurate representation of a complex system though, there are a lot of parameters that needs to be tuned, requiring a lot of data, usually constrained by the presence of sensors.

Generate synthetic data using a hybrid model

There are various methods to integrate data and physics, such as RC-models and physics-informed neural networks. While working on this article, I had a chance to watch this video by Steve Brunton, noting that many advanced deep neural network architectures are inspired by physics to steer the learning process using established knowledge of the world or to incorporate mathematical concepts. Without delving too deeply, it's noteworthy to mention architectures like ResNet (which mirrors the Euler Integrator), Lagrangian Neural Networks, and Fourier Neural Operators.

Conversely, some approaches involve adding a term to the loss function to balance adherence to data and physics. This concept is also applied in RC models, where data refines the parameters of a reduced-order model that still complies with well-understood physical laws representing the system.

Combining data and physics

Not all models are equal, particularly in simulating the physical world. Selecting the appropriate model is half of the job. By now, you have seen me mentioning digital twin multiple times in my previous articles. I believe that as long as we integrate sensor data with system dynamics, we essentially have a digital twin. The digital twin's unique advantage lies in its flexibility to balance data and physics as needed. While having a versatile tool means you can tackle various tasks, it often doesn't perform as well as a set of specialised tools. In my opinion this still holds true, and we should recognise the strength of each approach, understanding when and how to blend physics with data.

1. In case you are wondering why this introduction, I am citing this. It also gives me a chance to say that if the cadence of the newsletter is once every 3 weeks, the reason is that research takes time, and I’d rather publish what I consider “quality material” than at a higher cadence with lower quality.

2. This series about applied topology discusses what is the “shape of a dataset” and why it is important, it’s a fun watch.